Introduction

一个人能能走的多远不在于他在顺境时能走的多快，而在于他在逆境时多久能找到曾经的自己。 ————KMP

一次失败并不可怕，从失败中累积经验，让自己前进的步伐更快，成功的几率更高！ ————KMP

Before you compare with others,compare with yourself first！

​ ————KMP

String

有零个或多个字符组成的序列。

存储表示如下：

#define MAXLEN 255
typedef struct {
	char ch[MAXLEN];
	int length;
}SString;

串的存储有三种方式，

1. 把ch[0]用作锚点，用来记录串的长度。
2. ch[0]用来存数据，在末尾加一个\0。
3. 单独弄一个变量length专门来存串长。
4. 本方案是第一种和第二种的混合，即用length来存串长，ch[0]也没有存数据。

在我们考研书上用是第四种。故题目里面给的串，默认为ch[0]没用，还要单独列一个变量length。

简单模式匹配

故名思意，就是简单的字符串模式匹配。怎么简单粗暴怎么来，一个一个比对。

直接上代码，这个没啥理解难度。

int Index(SString S, SString T)
{
	int i = 1, j = 1;
    while(i <= S.length && j <= T.length)
    {
        if(S.ch[i] == T.ch[j])
        {
            j++;
            i++;
        }
        else
        {
            i = i - j + 2;
            j = 1;
        }
    }
    if(j > T.length)
        return i - T.length;
    else
        retorn 0;
}

KMP

通过上面的字符串匹配算法，有没有觉得非常的麻烦，每次都要从头再来，太慢了。

比如，下面的串第四个元素不匹配。

我们发现，虽然第四个对不上，但是前三个完全是可以对上的，能不能利用一下前三个，来降低比对的压力呢。

然后我们发现，如果，我们不把串回溯到头，只回溯到第2位，恰好是对的上的。

这就非常的amazing啊，可以省下一次比对，虽然少比对一个元素，但是给我们打开了思路。

比对开始

第一个不行

如果是比对的时候第一个元素就对不上，那么

立刻推，如同简单匹配算法一样，放过彼此，直接都进入下一个的比对

第二个不行

此时说明，第一个是可以的。如图

这种情况，可以把下面比对的串T移到T.ch[1]处，和上面的串S.ch[2]的元素比对。即(S.ch[2] ==T.ch[1]).

第三个不行

这里虽然前面两个可以，但是偷不了懒，因为移位之后，依然没有符合的。

所以，把T移到它的头部，再次进行比对。

第四次不行

这次我们可以偷懒了

由于前三个满足，第三个是a，第一个也是a，那是不是说明，S的第三个元素，一定等于T的第一个元素，我们这也就可以省一次比对。

第五次不行

同上，只能看出第四个和第一个相同，所以，我们可以这样移动。

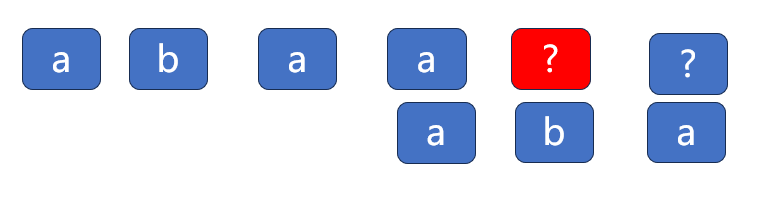
第六次不行

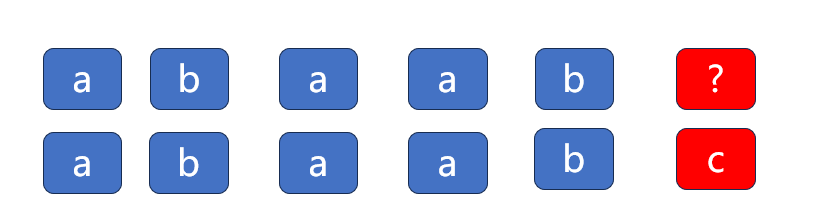
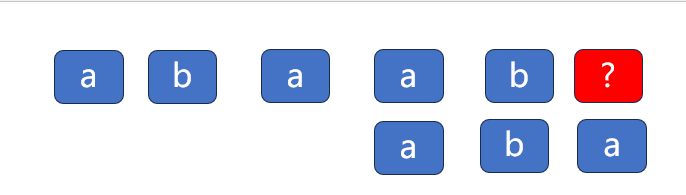
这次可以偷懒的地方多了，我们可以看到，S的第四和第五个元素分别是a和b，而T的第一和第二个元素也是a和b。所以，他们已经相等的情况下，我们就不需要比对了。

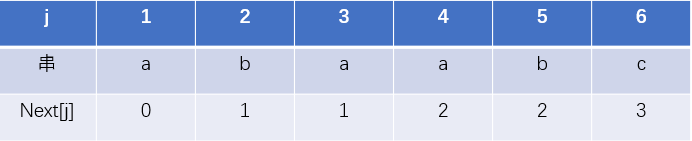
next数组

ok，上面的偷懒方法我就总结完成了。此时我们可以得到一个数组，记录了在哪个位置上出现问题时

移到相对应的位置。

这就被称为next数组。

代码

其实KMP的代码不难，和前面的简单模式匹配的代码差别不大。

int Index_KMP(String S, String T, int next[])
{
	int i = 1, j = 1;
    while(i <= S.length && j <= T.length)
    {
        if(j == 0||S.ch[i] == T.ch[j])
        {
            j++;
            i++;
        }
        else
        {
            j = next[j];
        }
    }
    if(j > T.length)
        return i - T.length;
    else
        retorn 0;
}

升级

虽然使用next数组让我们减轻了比对的负担，但是有的时候还是不能最大限度的偷懒。例如

当比对的字符串为aaaab时，用我们上面的方法算得的next数组就是

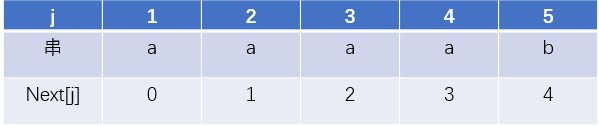
但是我们可以发现，第三个如果比对不成功，那待比对的字符S在3这个位置的元素绝对不会是a，而目标串T前面两个都是a，不可能对的上，我们完全可以偷懒不比对。

受限于next数组的这个限制，我们推出了nextval数组。

nextval第一位没什么可说的，和next数组一样，从第二位开始，如果第二位无法配对，那么我们根据next数组，我们需要把j的值定为1，但是此时T.ch[1]的值和T.ch[2]一模一样。第二位不能配对的值，在第一位也是绝对无法匹配，所以我们干脆直接让它去第一位的next数组指向的地方，少走弯路。

所以此时nextval数组就变成了

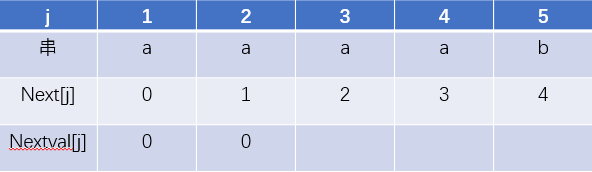
后面的3，4同样的到道理，第五位的时候，因为它的next数组的值是4，代表的元素是a和T.ch[5] = 'b'不相等，所以可以不用管。因此，我们得到的nextval数组就是

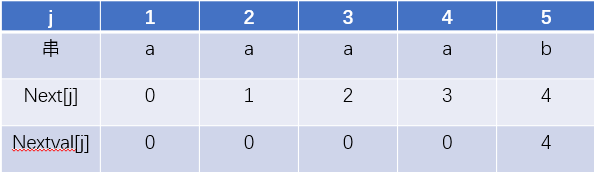
总结

KMP算法算是考研数据结构里面前三难的东西了，但却是相对最好得分的。考研KMP只需要会手算next和nextval数组就行了，而这理解了之后几乎没什么难度。

KMP算法本身的代码可以看一下，写一下，去年考过，也很简单，就是暴力匹配算法的换皮。